![Block Numbers]()
Iconic math can be expressed in three-dimensional manipulatives and interactive experiences. The Image shows the number 100 if each block were interpreted as multiplying what sits upon it by 2. The linear parens version of the iconic number is ((((((•)•)))•)). If each block were read to multiply what sits upon it by 10, then the image is a representation of the common number 1100100. If each ball were to represent a group of 5, then the number in the image would be 5500500. The iconic rules of transformation for block numbers is the same as the rules on the Parens Notation and the Container Numbers pages. Parens represents iconic numbers in the one-dimensional space of a textual line. Containers represent iconic numbers in the two-dimensional space of a planar page. Blocks represent the same iconic principles in the three-dimensional space of physical objects. By extruding two dimensional containment into a third direction, container numbers are converted into block numbers. The image of nested containment becomes one of stacked height.

Block Rules
Here are the whole numbers from –1 to 4 expressed as stack of blocks, with each block multiplying what rests upon it by two. For convenience on the rest of this page stacks of blocks are drawn in two-dimensions, as if looking upon the stack from the side. Conceptually these flatten stacks will be treated as if they were physical objects.

Next we transcribe the iconic transformation rules (Group, Merge and cancel) into behavioral interaction with the blocks. The physical embodiment of numbers as stacks comes with transformations that involve physically moving or removing blocks.

To illustrate these behavioral rules in action, here are the instructions (in blue) of how to standardize a unit-ensemble of four to a base-2 stack.
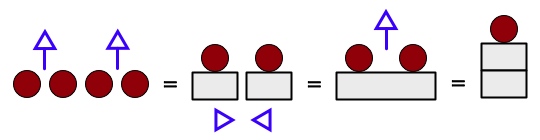
The up-arrow is the instruction to lift two units into a stack of one unit. The close-arrows instruct to push the blocks together.
This page is under construction, July 2013.
Block Addition
Two examples of block arithmetic addition follow. The first is 5+7.
Next, 5–6.
Block Multiplication